Одна маленькая деталь в виде пространственной решётки развернула жизнь математика из МГТУ имени Баумана и отца троих детей Дмитрия Соколова на 180 градусов. Программист исполнил мечту детства и стал изобретателем конструктора, в основе которого лежит декартова система координат.
В 1972 году в одном из институтов американского Университета Хопкинса (John Hopkins University) исследователи работали с группой талантливых ребят 12-15 лет. Дети были отобраны по следующим критериям: склонность к математике и развитое образное мышление. Участникам эксперимента предлагалось в ходе специальных математических тестов оперировать двух-трёхмерными объектами. В результате наблюдения за одарёнными школьниками учёные пришли к выводу, что умение конструировать даёт очевидное преимущество при решении задач любой сложности. Эксперимент повторяли из года в год.
Среди детей, побывавших на исследовании в Университете Хопкинса, были будущие нобелевские лауреаты, известные предприниматели и знаменитые творческие личности. Например, Марк Цукерберг и Леди Гага.
Примерно в то же время, когда в Университете Хопкинса начались эксперименты с математическими тестами и конструированием, на другой стороне Земли советский мальчик Дима, разбирая и собирая конструктор из ГДР, недоумевал, почему детали можно крепить только сверху и никак иначе. Полёт воображения просил как минимум трёхмерной реальности, но немецкий конструктор, как, впрочем, и все другие конструкторы, в которые Дима успел поиграть, не позволяли фантазии разгуляться.
Как и его американские ровесники, советский школьник был юным математическим дарованием. По объективным причинам путь его не мог пройти через Университет Хопкинса, но, к счастью, прошёл через знаменитую московскую школу номер 57, куда Дмитрий Соколов поступил после 8 класса, и где родилась в некотором смысле любовь всей его жизни — увлечение геометрией.
"Геометрию я любил и раньше, а учёба в школе № 57 закрепила мою страсть: в этой школе подготовка по математике была (и остаётся) одной из лучших в стране, если не самой лучшей, — вспоминает Дмитрий Соколов. – Свою идею сделать конструктор, который мог бы достраиваться во все стороны абсолютно одинаково, я сформулировал, в первую очередь, как геометрическую задачу. Необходимо было разбить трёхмерное пространство на две одинаковые регулярные пространственные решётки, которые, переплетаясь, заполняли бы его полностью".
Регулярность означала, что одна и та же деталь соответствует любой части решётки. Принцип переплетения позволял деталям, находящимся в разных решётках, держаться на трении при соприкосновении друг с другом. Принцип одинаковости означал, что детали при соединении попадают в любую решётку. Заполнение всего пространства предполагало, что деталь при сборке можно поместить в любую точку, а значит, создать любую произвольную фигуру.
"Решение поставленной геометрической задачи и было главным фундаментом в изобретении конструктора, — отмечает Дмитрий Соколов. – Поиск ответа происходил исключительно в моём пространственном воображении".
Вот точное математическое определение, к которому пришёл изобретатель. Трёхмерное пространство. Декартова система координат. Обе решётки кубические. Узлы первой решетки лежат в точках, у которых все три координаты чётные числа (0 тоже считаем чётным числом). В каждой точке пространства с тремя чётными координатами расположен узел первой решётки. Узлы второй решётки лежат в точках, у которых все три координаты нечётные числа. В каждой точке пространства с тремя нечётными координатами расположен узел второй решётки.
Рёбра решёток параллельны осям координат. Рёбра решёток являются объёмными телами. Сечение ребра, перпендикулярное линии, соединяющей соседние узлы, представляет собой квадрат со стороной единичной длины. Причём линия, соединяющая соседние узлы, проходит через центр квадрата, а стороны квадрата параллельны осям координат.
Конфигурация пустот в этой решетке полностью повторяет саму решетку. А это значит, что, во-первых, при параллельном переносе первой решётки на вектор она полностью совпадет со второй решёткой и, во-вторых, обе решётки вместе полностью заполняют трёхмерное пространство. Таким образом, не существует точки пространства, не принадлежащей ни одной из решёток.

К моменту, когда идея конструктора нашла геометрическое решение и приобрела реальные черты, изобретатель уже закончил МГТУ им. Баумана, сделал карьеру программиста и на одном из этапов своего профессионального пути отлаживал системные процессы на подмосковном Храпуновском инструментальном заводе (ХИЗ).
Предприятие некогда лидировало в СССР по выпуску металлорежущего инструмента, но с развалом Советского Союза переквалифицировалось и занялось упаковочной продукцией. Именно здесь два года назад поверили в уникальную идею и решили запустить производство конструктора из экологически чистого и безопасного пластика АБС, с использованием немецких гранул и уникальных пресс-форм.
В 2014 году, когда были выпущены самые первые комплекты конструктора, начались тесты изобретения в школах и детских садах Москвы и Подмосковья. План по захвату Вселенной Дмитрия Соколова состоял не только в том, чтобы превзойти конкурентов, но ещё и в том, чтобы создать продукт, который поможет детям развивать креативное мышление и станет им существенной подмогой на пути получения образования, а затем и профессиональной реализации.
Идея об интеллектуальной пользе конструктора оказалась востребованной и после серии испытаний подтвердилась.
"Помимо базовых умений (настраиваться и погружаться в работу, эффективно участвовать в процессе обсуждения) у учащихся формируются специальные умения: находить нестандартные решения творческих задач, которые помогают каждой работе стать индивидуальной и неповторимой", — делится своими выводами Татьяна Маркова, педагог московской школы номер 26, по результатам занятий в младших классах.
Положительную динамику по итогам кружка на основе нового конструктора отмечает и педагог лицея 1561 в Москве Елена Бриллинг. По её словам, дети 8-9 лет после десяти занятий быстрее осваивают схемы слов, предложений, видят структуру текста, легко оперируют классификациями/обобщениями, их рисунки становятся более детализированными, легче усваиваются/запоминаются алгоритмы действий (особенно на уроках информатики, на математике — последовательность записи решения примеров, схемы записи задач, на русском — разбор слова), лучше становится зрительно-моторная координация.
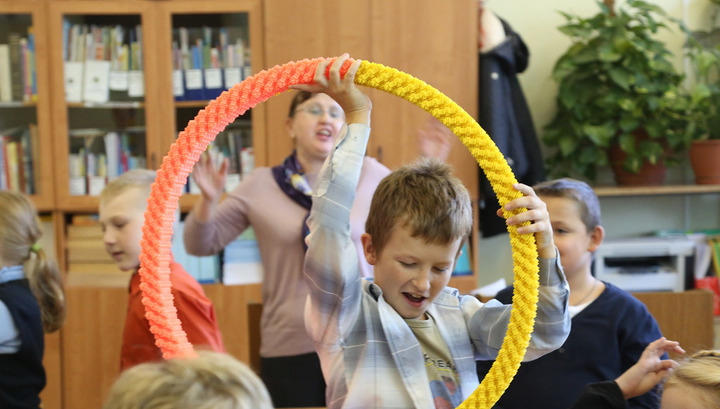
В завершившемся учебном 2016-2017 году конструктор, появившийся на свет из любви к геометрии, вписался в образовательный процесс в России на правах полноценного участника. Среди достижений проекта — олимпиады, образовательные выставки, мастер-классы и технопарки с географией от Ялты и Гатчины до Мурманска и Владивостока.
При этом ещё чуть более года назад конструктор выходил в виде всего восьми тематических наборов, а сейчас их счёт идёт уже на третий десяток. На сайте проекта есть 3D-конструктор, который позволяет на экране планшета или компьютера создавать виртуальные модели и инструкции по сборке.
В обозримом будущем создатели хотят сделать первые шаги в модную сегодня робототехнику. Так, в новую линейку конструктора, которая выйдет в начале 2018 года, добавят динамические элементы, которые в будущем можно будет объединять с сенсорами и датчиками и создавать инженерные проекты.
Сегодня продукт интеллектуального труда Дмитрия продаётся более чем в ста городах по всей России, а также в Испании, Чехии, Германии, Бельгии, Великобритании, Белоруссии и Латвии, Австралии, Канаде и США.
Добавим, что в наши дни детей, собственно, как и многих взрослых, можно увлечь не только 3D-конструктором. На просторах Интернета можно найти набор для создания новой формы жизни, поучаствовать в обучении роботов, решении квантовых проблем, помочь раскрыть структуру сложнейшего белка и побороть туберкулёз.
Все дети имеют таланты. Задача взрослого — дать развиться потенциалу, заинтересовать, показать, какие возможности открываются сегодня перед самыми обычными подростками. Ведь именно такие уверенные в себе люди будут улучшать наш мир завтра. Дмитрий Соколов — прекрасный тому пример.